Kosmologie: verschil tussen versies
(Introductie in de Kosmologie) |
k (→{{4.gif}} '''''De leeftijd van het heelal''''': WFL (Par. wetenschap) verwijderd.) |
||
| (3 tussenliggende versies door 2 gebruikers niet weergegeven) | |||
| Regel 1: | Regel 1: | ||
| − | Een introductie in de '''Kosmologie'''. | + | Een introductie in de '''Kosmologie'''.<br> |
In dit stuk wordt een introductie gegeven in de Kosmologie. | In dit stuk wordt een introductie gegeven in de Kosmologie. | ||
| Regel 244: | Regel 244: | ||
| − | [[Categorie:natuurkunde]] | + | ==={{4.gif}} '''''De wet van Hubble en de mate van uitdijing'''''=== |
| + | |||
| + | De golflengteverandering van het licht kan worden vergeleken met de veranderingen van het geluid van bewegende objecten: wanneer een ambulance met loeiende sirene op ons af rijdt, is het geluid hoger dan wanneer de ambulance zich van ons verwijdert. | ||
| + | De roodverschuiving van het licht is gelijk aan de verwijderingssnelheid gedeeld door de snelheid van het licht. | ||
| + | Als de verwijderingssnelheid niet te groot is, kan de kosmische roodverschuiving worden voorgesteld door de wet van Hubble, die de relatieve verwijderingssnelheid en de onderlinge afstand van twee sterrenstelsels met elkaar in verband brengt: | ||
| + | |||
| + | Snelheid = H<sub>0</sub> x afstand | ||
| + | |||
| + | Zoals ook in het elastiekmodel werd ge�llustreerd, bewegen stelsels zich sneller van elkaar weg wanneer ze verder van elkaar verwijderd zijn. | ||
| + | De wet van Hubble geeft de werkelijkheid goed weer, zoals uit het Hubble-diagram blijkt. | ||
| + | |||
| + | [[Afbeelding:hubble_s.jpg]] | ||
| + | |||
| + | In dit diagram worden afstand en snelheid of roodverschuiving tegen elkaar uitgezet. | ||
| + | Het getal H<sub>0</sub> in deze formule is de Hubble-constante, die gevonden kan worden door niet relatieve afstanden maar absolute afstanden te bepalen. | ||
| + | Als de wet van Hubble klopt, kunnen we de Hubble-constante bepalen door de verwijderingssnelheid (of roodverschuiving) en de afstand van het sterrenstelsel tot ons te meten. | ||
| + | Snelheden kunnen zeer precies bepaald worden aan de hand van de roodverschuiving van het licht. | ||
| + | Afstanden kunnen ook nauwkeurig bepaald worden, als ze niet te groot zijn, en wel met behulp van driehoeksmeting, een techniek die ook door landmeters wordt gebruikt. | ||
| + | |||
| + | [[Afbeelding:parallax.gif]] | ||
| + | |||
| + | De afstand tot nabije sterren kan berekend worden door de omloopbaan van de aarde als basislijn te nemen; de gezochte afstand vind je door de kleine verschillen in positie door het jaar heen te meten ten opzichte van zeer ver weg gelegen sterren. | ||
| + | Hiermee kunnen kleine kosmische afstanden worden berekend, maar voor grote afstanden is deze methode niet bruikbaar (de hoeken zijn daarvoor te klein). | ||
| + | En aangezien de wet van Hubble geldt voor globale bewegingen op grote schaal, is het om de Hubble-constante te kunnen bepalen noodzakelijk om de grote afstanden nauwkeurig te meten, wat technisch een zeer moeilijke opgave is. | ||
| + | Dat is de reden dat de waarde van de Hubble-constante nog altijd een onzekerheidsmarge van ongeveer 20 procent heeft, hoewel het lieaire karakter van de wet van Hubble al wel tamelijk nauwkeurig is aangetoond. | ||
| + | De waarde van de Hubble-constante is belangwekkend omdat hij ons vertelt hoe snel objecten zich van elkaar verwijderen. | ||
| + | Omdat de verwijderingssnelheid recht evenredig is met de afstand, zou elk sterrenstelsel er, in omgekeerde richting, even lang over doen om de afstand naar willekeurig welk ander sterrenstelsel te overbruggen. | ||
| + | Met ��n enkel getal, het omgekeerde van de Hubble-constante, 1/H[sub]0[/sub], kan dus uitgedrukt worden hoe lang geleden alle sterrenstelsels 'op dezelfde plaats' waren, aangenomen dat de uitdijingssnelheid altijd gelijk is geweest (discutabel). | ||
| + | Volgens de huidige berekeningen ligt 1/H[sub]0[/sub] tussen de 14 en 17 miljard jaar. | ||
| + | Als de sterrenstelsels nooit van snelheid zijn veranderd, moeten ze zich zo lang geleden op punt 0 hebben bevonden en is dit de hoeveelheid tijd die is verstreken sinds de oerknal. | ||
| + | |||
| + | |||
| + | ==={{4.gif}} '''''Veranderingen in de uitdijingssnelheid'''''=== | ||
| + | |||
| + | Maar sterrenstelsels, en de pregalactische materie daarvoor, hebben niet altijd dezelfde uitdijingssnelheid gehad. | ||
| + | De snelheid is be�nvloed door de zwaartekracht. | ||
| + | Wanneer je een voetbal de lucht in schiet, zal hij terugvallen naar de aarde, behalve wanneer hij zeer hard wordt geschoten: dan zal hij worden afgeremd maar nooit terugvallen en zich eeuwig verwijderen van de aarde. | ||
| + | Dezelfde opties gelden voor het heelal; het zijn ook dezelfde wiskundige vergelijkingen die de beweging van de voetbal en de verwijdering van twee sterrenstelsels beschrijven. | ||
| + | Het natuurkundige principe is hetzelfde: in beide gevallen wordt de beweging bepaald door de zwaartekracht. | ||
| + | Het enige verschil is dat de beweging van de bal wordt bepaald door de zwaartekracht van de aarde en de beweging van de sterrenstelsels door de zwaartekracht van hun eigen massa en die van ander materiaal in het heelal. | ||
| + | Vergelijkbaar met de zacht geschoten bal is een langzaam uitdijend heelal met een grote dichtheid. | ||
| + | De uitdijingssnelheid van zo'n heelal neemt af tot de uitdijing uiteindelijk stopt; daarna krimpt het weer in en beginnen alle sterrenstelsels naar elkaar toe te bewegen om te eindigen in een 'eind-krak'. | ||
| + | De hard geschoten bal is vergelijkbaar met een snel uitdijend heelal met een lagere dichtheid dat eeuwig blijft uitdijen. | ||
| + | De sterrenstelsels dunnen dusdanig uit dat de zwaartekracht niet veel effect meer heeft. | ||
| + | Wanneer zo'n heelal zeer oud wordt, neemt de uitdijingssnelheid nauwelijks nog af en blijft het heelal met een bepaald kruissnelheid uitdunnen. | ||
| + | Tussen deze twee scenario's ligt het delicate evenwicht van een heelal dat te vergelijken is met de voetbal die precies de ontsnappingssnelheid heeft meegekregen: het juiste evenwicht tussen snelheid en dichtheid zorgt ervoor dat het heelal eeuwig snelheid 0 nadert maar nooit bereikt. | ||
| + | |||
| + | Net als met de bal is het moeilijk te bepalen welk scenario voor het heelal geldt alleen door naar de situatie op een bepaald moment te kijken. | ||
| + | Als de bal maar een klein stuk omhoog wordt geschoten, zal hij direct weer terugvallen, maar als hij hard wordt geschoten, zal hij zeer ver komen voordat hij terugkeert - en het is moeilijk te zeggen �f hij zal terugkeren. | ||
| + | Ook een heelal kan zeer lang uitdijen voordat het, als dat al gebeurt, weer gaat inkrimpen. | ||
| + | Als dat het lot van ons heelal is, zal het eerst tientallen miljarden jaren hebben bestaan. | ||
| + | De ontsnappingssnelheid van de bal is afhankelijk van de massa van de aarde en van de hoogte waarvandaan hij geschoten is. | ||
| + | Zo is ook het lot van het heelal afhankelijk van de snelheid waarmee het uitdijt en de hoeveelheid massa die de uitdijing vertraagt. | ||
| + | Deze waarden zijn nog niet exact genoeg bepaald om te kunnen weten wat er gebeuren zal. | ||
| + | De beste methode om ze te bepalen is door de expansiesnelheid in het verleden vast te stellen (door zeer ver weg te kijken) en deze te vergelijken met de huidige snelheid. | ||
| + | De gegevens zijn nog niet betrouwbaar genoeg om te kunnen zeggen dat de uitdijingssnelheid afneemt, maar er zijn veelbelovende technieken. | ||
| + | |||
| + | Het heelal heeft echter nog een optie die de bal niet heeft, namelijk om steeds sneller te gaan uitdijen, zoals een bal in een slingerworp of een raket. | ||
| + | Dit is in principe mogelijk doordat de zwaartekracht als een afstotende kracht kan inwerken op lege ruimte. | ||
| + | Einstein introduceerde deze mogelijkheid van een 'kosmologische constante' kort na zijn gravitietheorie. | ||
| + | Deze treedt op als lege ruimte zonder materie of straling toch energie bevat, waarop de zwaartekracht aangrijpt. | ||
| + | Als het vacu�m genoeg energie heeft, zal de kracht die het heelal uiteendrijft de zwaartekracht overvleugelen en zal de uitdijingssnelheid met de tijd toenemen. | ||
| + | Deze optie is al sinds de ontdekking van de uitdijing bekend, maar we weten nog altijd niet zeker of de uitdijingssnelheid toeneemt of afneemt (hoewel de laatste onderzoeken het eerste aantonen). | ||
| + | Alleen door de dynamica op zeer grote schalen te onderzoeken lijkt het mogelijk om de energie van het vacu�m te bepalen. | ||
| + | |||
| + | |||
| + | ==={{4.gif}} '''''De leeftijd van het heelal'''''=== | ||
| + | |||
| + | Zelfs als we de Hubble-constante en de Hubble-tijd (de tijd die alle sterrenstelsels nodig hadden om te komen waar ze nu zijn met hun huidige snelheid) kennen, weten niet precies hoe oud het heelal is. | ||
| + | De leeftijd is afhankelijk van de veranderingen in de uitdijingssnelheid door de tijd heen, en die zijn weer afhankelijk van de soorten en de hoeveelheid materie die het heelal bevat. | ||
| + | Maar we kunnen het omdraaien: als we de leeftijd met de Hubble-tijd ons iets vertellen over de aard van het universum en de toekomst ervan. | ||
| + | We weten vrij nauwkeurig hoe oud ons zonnestelsel is: de zon, de aarde en andere planeten zijn ongeveer 4,55 miljard jaar geleden uit interstallair gas gevormd. | ||
| + | Deze schatting is gebaseerd op metingen van radioactief verval. | ||
| + | De atoomkernen van sommige elementen, zoals uranium-238, zijn instabiel en verallen tot atoomkernen van andere elementen. | ||
| + | Dat doen ze met een bepaalde snelheid die heel precies te bepalen is. | ||
| + | Na 4,6 miljard jaar bijvoorbeeld heeft een atoom uranium-238 50 procent kans om te zijn vervallen tot lood-206 en bestaat een oorspronkelijk pure klomp uranium-238 voor de helft uit lood-206. | ||
| + | Als we dus vrij voorkomende stukken steen en meteorieten die uranium bevatten maar zonder lood-206 zijn begonnen (of met een hoeveelheid andere isotopen van lood), dan is uit het percentage lood-206 af te leiden hoe lang geleden het uranium werd gevormd. | ||
| + | Zeer veel objecten uit ons zonnestelsel, vooral meteorieten, zijn onderzocht op verschillende soorten radioactief verval (bijvoorbeeld van kalium-40 naar argon-40; halveringstijd 1,3 miljard jaar). | ||
| + | Alle berekeningen komen uit op dezelfde leeftijd van 4,55 miljard, dus het zonnestelsel is minstens zo oud. | ||
| + | |||
| + | Hoewel er nog steeds sterren worden gevormd, zijn er vele die ouder zijn dan ons zonnestelsel. | ||
| + | Sommige zijn twee tot drie keer zo oud en het is waarschijnlijk dat een aantal van de eerste sterren die ontstaan zijn na deoerknal nu nog brandt. | ||
| + | We kunnen deze sterren gebruiken om te schatten hoe oud het heelal is. | ||
| + | |||
| + | Het zou prettig zijn geweest als iemand een stopwatch had aangezet bij de oerknal en hem voor ons had achtergelaten zodat wij gewoon de hoeveelheid tijd die is verstreken konden aflezen. | ||
| + | In feite hebben we iets wat hierop lijkt: oude groepen sterren met een grote verscheidenheid aan massa's die als een soort zandlopers met verschillende snelheden lopen. | ||
| + | Als we dus in staat zijn sterren als zandlopers te lezen, dat wil zeggen: te bepalen hoe oud ze zijn aan de hand van onze kennis van hun levensloop, dan kunnen we ook de leeftijd van de clusters waartoe ze behoren bepalen door naar de zandlopers te kijken die bijna leeggelopen zijn. | ||
| + | Om dat te kunnen doen hebben we een model van de werking van sterren nodig. | ||
| + | |||
| + | Sterren als onze zon, die genoeg brandstof hebben. blijven miljarden jaren stabiel. | ||
| + | Het zijn gasbollen die grotendeels bestaan uit waterstofatomen en vrije elektronen en die bijeen worden gehouden door de zwaartekracht en voor instorten behoed door de hitte van de nucleaire reacties in hun kern. | ||
| + | De meeste sterren brengen het grootste deel van hun leven door in deze fase en de meeste sterren die wij aan de hemel zien bevinden zich in deze fase. | ||
| + | |||
| + | Maar deze stabiele toestand eindigt uiteindelijk. | ||
| + | Het evenwicht dat de ster in stand houdt, begint te wankelen wanneer de waterstof in de kern, die als brandstof dient, begint op te raken. | ||
| + | Door dit tekort stort de kern in. | ||
| + | Hierbij komt meer hitte vrij dan nodig is om de buitenste lagen in stand te houden zodat deze naar buiten worden gedreven. | ||
| + | De structuur van de ster verandert dus als de waterstof opraakt: de kern wordt kleiner, de buitenste lagen groter. | ||
| + | De effecten hiervan zijn zichtbaar in het licht dat de ster uitzendt. | ||
| + | Omdat het licht afkomstig is van een groter gebied, is het meer verspreid, waardoor ook de temperatuur anders is. | ||
| + | De ster wordt koeler en zijn licht wordt roder. | ||
| + | |||
| + | Sterren lijken op zandlopers omdat ze vanaf het moment dat ze zijn gevormd hun brandstof beginnen te verbruiken. | ||
| + | Wanneer die begint op te raken veranderen ze van kleur. | ||
| + | Zware sterren schijnen helderder dan lichte en verbruiken hun brandstof sneller (ze werken als snellere zandlopers). | ||
| + | Van een groep sterren zullen de zwaarste dus het eerste uitdoven. | ||
| + | Door de massa te meten van de sterren die net door hun brandstof heen zijn, kunnen we de leeftijd van de cluster vaststellen. | ||
| + | |||
| + | We kunnen sterren aflezen als klokken omdat we weten hoe ze zich ontwikkelen. | ||
| + | Er zijn modellen ontwikkeld die voor elke massa en samenstelling van een ster bepaalde waarneembare eigenschappen (helderheid en kleur) voorspellen bij een bepaalde leeftijd. | ||
| + | Uit de helderheid en kleur van een ster kunnen we dus afleiden hoe lang geleden hij is gevormd. | ||
| + | De nauwkeurigheid van deze modellen is bevestigd door andere tests. | ||
| + | De voorspelde leeftijd van de zon komt bijvoorbeeld overeen met de resultaten van datering met behulp van radioactief verval. | ||
| + | En als de massa van een ster bekend is, kunnen de helderheid en kleur ervan voorspeld worden. | ||
| + | Er is zelfs een geval bekend waarbij twee om elkaar draaiende sterren met een verschillende massa volgens de berekeningen even oud zijn. | ||
| + | |||
| + | Momenteel wordt de leeftijd van de oudste sterrenhopen geschat op 12 tot 15 miljard jaar. | ||
| + | De oudste sterrenhopen lijken maar een paar miljard jaar van elkaar te verschillen in leeftijd en er is niet veel gevonden wat ouder is dan dit - een opmerkelijk feit, wat waarschijnlijk betekent dat het heelal ongeveer zo oud is. | ||
| + | Nog opmerkelijker is dat deze leeftijd overeenkomt met de expansietijd van 14 tot 17 miljard jaar die is afgeleid van de Hubble-constante. | ||
| + | We hebben nu dus een behoorlijk betrouwbaar beeld van de kosmische chronologie, al zijn de marges nog vrij ruim. | ||
| + | |||
| + | Als we goed naar de getallen kijken, lijken de sterren in sommige modellen van de uitdijing (bijvoorbeeld de modellen waarbij het heelal weer gaat inkrimpen omdat de zwaartekracht de uitdijingssnelheid continu vertraagt) ouder te zijn dan het heelal. | ||
| + | De voorspelde leeftijd van het heelal in alle 'eindkrakmodellen' is maximaal (2/3)/H[sub]0[/sub], ongeveer 10 miljard jaar. | ||
| + | De leeftijd in deze modellen is betrekklijk jong omdat er wordt aangenomen dat de sterrenstelsels vroeger sneller uiteenvlogen dan nu. | ||
| + | Ze hebben er dus minder lang over gedaan om te komen waar ze nu zijn en voorspellen dus een te jong heelal. | ||
| + | |||
| + | Het heelal kan oud zijn als de dichtheid van de materie laag is, zodat de uitdijing de laatste 10 miljard jaar nauwelijks door de zwaartekracht is vertraagd. | ||
| + | En als de uitdijing zich heeft versneld ten opzichte van de kosmologische constante, dan voltrok zij zich daarvoor langzamer en kan het heelal nog ouder zijn. | ||
| + | Hoe het ook zij, volgens de huidige opvattingen is er niet genoeg zwaartekracht om de uitdijing te stoppen en om te keren. | ||
| + | Het heelal zal waarschijnlijk nog zeer lange tijd uitdijen, en mogelijk zelfs voor eeuwig. | ||
| + | |||
| + | Het naakte feit van de uitdijing impliceert dat de materie ooit een veel grotere dichtheid had dan nu. | ||
| + | Het huidige verloop van de uitdijing vertelt ons echter niet veel over het gebeuren tijdens de eerste miljard jaar, de eerste miljoen jaar, de eerste minuten, de eerste seconden. | ||
| + | De twee belangrijkste bronnen van informatie over deze perioden van de kosmische geschiedenis zijn de kosmische achtergrondstraling en de samenstelling van de oermaterie. | ||
| + | |||
| + | |||
| + | |||
| + | [[Categorie:natuurkunde]] | ||
| + | [[Categorie:Wetenschap]] | ||
Huidige versie van 3 dec 2005 om 20:29
Een introductie in de Kosmologie.
In dit stuk wordt een introductie gegeven in de Kosmologie.
Inhoud
- 1 Geschiedenis van het heelal
- 2 Het uitdijen van het heelal
- 2.1 http://forum.fok.nl/templates/foksilver/i/p/5.gif Dijt alles uit?
- 2.2 http://forum.fok.nl/templates/foksilver/i/p/5.gif Bevinden wij ons in het centrum van het Heelal?
- 2.3 http://forum.fok.nl/templates/foksilver/i/p/5.gif Waartoe leidt de uitdijing?
- 2.4 http://forum.fok.nl/templates/foksilver/i/p/5.gif Wat gebeurde er voor de oerknal?
- 2.5 http://forum.fok.nl/templates/foksilver/i/p/5.gif Heeft de tijd zelf een begin gehad?
- 2.6 http://forum.fok.nl/templates/foksilver/i/p/4.gif Effecten van de uitdijing op licht.
- 2.7 http://forum.fok.nl/templates/foksilver/i/p/4.gif De wet van Hubble en de mate van uitdijing
- 2.8 http://forum.fok.nl/templates/foksilver/i/p/4.gif Veranderingen in de uitdijingssnelheid
- 2.9 http://forum.fok.nl/templates/foksilver/i/p/4.gif De leeftijd van het heelal
Geschiedenis van het heelal[bewerken]
http://forum.fok.nl/templates/foksilver/i/p/4.gif Het Vacu�mtijdperk[bewerken]
- Het Planck-tijdperk (tijd 10-43 seconde, temperatuur 1019 GeV).
- Dit tijdperk kan worden gezien als het begin van de tijd, want voorbij deze grens is het concept 'tijd' niet meer zinvol.
- Tijd is niet uit te drukken in eenheden kleiner dan de Planck-tijd, dus het heeft geen zin om te spreken van 'voor' deze tijd; de ::begrippen 'tijd' en 'ruimte' zijn niet duidelijk van elkaar te onderscheiden bij kleinere eenheden.
- Waarschijnlijk zijn alle waarneembare overblijfselen uit dit tijdperk weggevaagd door de inflatie (exponenti�le uitdijing), behalve ::dan de ontstane ruimtetijd zelf.
- Het inflatietijdperk (na het Planck-tijdperk en voor 10-10 seconde, temperatuur 100 GeV).
- Het fysieke vacu�m domineert de energie en doet een afstotende zwaartekracht ontstaan die het heelal opblaast tot enorme ::afmetingen.
- Dit kan worden beschouwd als de 'knal' zelf aangezien we het effect ervan, de kosmische uitdijing, nog steeds waarnemen.
- Het is mogelijk, maar nog niet bewezen, dat dit proces de fluctuaties heeft veroorzaakt die hebben geleid tot de vorming van ::sterrenstelsels en alle andere niet-homogene structuren die nu in het heelal bestaan.
- Als dat zo is, kunnen we misschien overblijfselen uit deze tijd vinden in de fluctuaties van de microgold-achtergrondstraling of in ::de vorm van zwaartekrachtstraling uit de 'oer-tijd'.
http://forum.fok.nl/templates/foksilver/i/p/4.gif Het Stralingstijdperk[bewerken]
- Het ontstaan van licht (na de inflatie en voor het ontstaan van materie, temperatuur hoger dan 100 GeV).
- De vacu�menergie transformeert en neemt de vorm aan van bekende deeltjes als fotonen en andere lichtquanten en van materie- en ::antimateriedeeltjes (in even grote hoeveelheden).
- In dit tijdperk wordt energie omgezet in thermische straling.
- De afstotende zwaartekracht verdwijnt en de zwaartekracht krijgt zijn huidige, aantrekkende karakter.
- De achtergrondstraling die momenteel overal in het heelal aanwezig is, komt hiervandaan.
- Het is mogelijk dat de donkere materie ook in deze vroege tijd is ontstaan en het grootste deel van de massa van het huidige heelal ::vormt.
- Het ontstaan van baryonische materie (na het ontstaan van licht en voor of tijdens het elektrozwakke tijdperk, temperatuur 100 :GeV).
- Een iets grotere hoeveelheid quarks en elektronen dan antiquarks en anti-elektronen onstaan in een proces dat baryogenese wordt ::genoemd.
- Dit proces heeft zijn sporen nagelaten in de huidige aanwezigheid (en overvloed) van baryonische materie, waartoe alle gewone ::materie (alle atomen in alle sterren en sterrenstelsels) behoort.
- Het elektrozwakke tijdperk (tijd 10-10 seconde, temperatuur 100 GeV).
- Dit tijdperk markeert de overgang naar het huidige, in laberatoria geteste natuurkunde.
- Met andere woorden: de hiervoor genoemde fenomenen worden eerder gebruikt als kosmologische toetstenen voor onze natuurkundige ::theorie�n dan omgekeerd.
- Maar ook in andere opzichten is deze periode belangrijk.
- Zij markeert bijvoorbeeld de overgang van het vacu�m naar de toestand waarin deeltjes hun rustmassa krijgen; het is misschien de ::tijd waarin baryonische materie ontstaat en waarin de suppersymmetrie van het vacu�m eindigt, waarna materie en krachten ::onderscheidbare vormen van energie met verschillend gedrag worden.
- Er zijn misschien kosmische overblijfselen van deze periode (zoals donkere materie of kosmische 'weeffouten'), maar misschien ook ::niet.
- Het sterke tijdperk (tijd 10-4 seconde, temperatuur 0,2 GeV).
- Ongeveer op dit moment ondergaat het heelal de overgang van 'quarksoep' naar hadronische materie, waarin quarks en gluonen hun ::huidige vorm krijgen en uitsluitend in neutronen en protonen huizen.
- Overblijfselen van deze overgang zijn misschien bepaalde soorten donkere materie (axionen, zwarte gaten of 'quarkklontjes'); ook ::kan het de materie een niet-homogene structuur hebben gegeven, die van invloed is geweest op de latere vorming van atoomkernen.
- Ontkoppeling van de zwakke wisselwerking (tijd 1 seconde, temperatuur 1 MeV).
- Neutronen en protonen kunnen niet meer ongehinderd in elkaar overgaan.
- Het belangrijkste gevolg hiervan is dat er ongeveer zeven keer zoveel protonen als neutronen zijn, wat weer tot gevolg heeft dat ::het heelal grotendeels uit waterstof bestaat.
- De talrijke achtergrondneutrino's die sindsdien zonder interacties op ons toe stromen, hebben toen hun dichtheid gekregen.
- Verschillende mogelijke vormen van donkere materie onttrekken zich op dit moment aan de interacties met normale materie en hun ::hoeveelheden komen vast te liggen.
- Kort daarna vindt de laatste grote vernietiging van antimaterie plaats: elektronen en positronen dumpen hun hitte in de ::achtergrondfotonen, die daardoor nu iets meer energie hebben dan neutrino's.
- Ontstaan van de atoomkernen van lichte elementen (tijd 100 seconden, temperatuur 0,1 MeV).
- De afkoeling die heeft plaatsgehad, maakt het mogelijk dat protonen en neutronen aan elkaar vast blijven zitten.
- Dit proces wordt nucleosynthese genoemd.
- Het overgrote deel van alle neutronen vormt samen met protonen heliumkernen, van het restant vormt het grootste deel ::deuteriumkernen, wat dan nog overblijft vormt lithium en een verwaarloosbare hoeveelheid zwaardere elementen.
- De momenteel aanwezige hoeveelheden van deze elementen bevestigen ons beeld van deze fase.
- Ontkoppeling van het stralingsspectrum (tijd vanaf 1 maand, temperatuur 500 eV).
- Terwijl het heelal uitdunt, neemt de interactie tussen de materie en straling af.
- Het zeer precieze spectrum van de achtergrondstraling die we nu waarnemen, heeft in deze tijd zijn beslag gekregen; slechts weinig ::energie kan daarna nog ongemerkt zijn toegevoegd.
- De ontkoppeling gebeurt in fasen: de productie van fotonen eindigt vroeg, terwijl de energieuitwisseling tussen de deeltjes nog een ::tijdlang doorgaat.
- De laatste fase van de omzetting van de oorspronkelijke energie in de meeste achtergrondfotonen die we nu waarnemen, vindt plaats.
http://forum.fok.nl/templates/foksilver/i/p/4.gif Het Materietijdperk[bewerken]
- Materie wordt dominant boven straling (tijd ongeveer 10.000 jaar, temperatuur 30.000 K, ofwel 3eV).
- De materie van het heelal verliest minder energie aan de expansie dan de straling en vormt uiteindelijk een groter deel van de ::massadichtheid.
- De baryonische materie wordt nog steeds sterk beheerst door de intense druk van de hete straling, maar het grootste deel van de ::zwaartekracht en de massa worden gevormd door donkere materie, die ongeveer vanaf deze tijd vrijelijk kan bewegen.
- In dit tijdperk onstaan fluctuatie in de dichtheid van de kosmische massa, die de basis leggen voor de huidige grootschalige ::verspreiding van materie.
- Laatste verstrooiing (tijd ongeveer 500.000 jaar, temperatuur ongeveer 3000 K).
- Wanneer de straling zo ver is afgekoeld dat de elektronen zich met protonen kunnen verbinden ('waterstofrecombinatie'), vindt er ::vrijwel geen wisselwerking meer plaats tussen elektronen en straling.
- De straling plant zich hierna vrij voort door de ruimte.
- We kunnen dit tijdperk direct waarnemen met behulp van onze kaarten van de kosmische achtergrond, dus naarmate er betere kaarten ::worden gemaakt, zullen we meer details over deze tijd te weten komen.
- De baryonische materie, losgekoppeld van de straling, beweegt vanaf deze tijd vrij rond: de groei van de kosmische structuur wordt ::niet meer door de straling belemmerd.
- De donkere tijd (tot ongeveer 1 miljard jaar, temperatuur ongeveer 0,002 eV, ofwel 20 K).
- De zwaartekracht van de materie heeft een versterkende invloed op de oorspronkelijke fluctuaties in de donkere en de baryonische ::materie, maar deze structuren zijn lange tijd niet meer dan kleine rimpelingen.
- Ergens in deze periode vormen de hevigste rimpelingen de eerste niet-lineaire structuren (de eerste structuren die niet meer ::uitdijen), waarschijnlijk stelsels met ongeveer een miljoen keer de massa van de zon.
- De vorming van sterrenstelsels (aanvang vanaf ongeveer 1 miljard jaar, temperatuur ongeveer 0,002 eV, ofwel 20 K).
- Door de zwaartekracht worden de 'rimpelingen' steeds groter.
- De grootste golven worden uiteengeslagen en leiden tot de vorming van de eerste sterrenstelsels.
- Gas stort ineen tot sterrenstelsels en vormt zeer snel sterren en quasars met zo'n grote helderheid dat we ze ook nu nog kunnen ::waarnemen.
- Het licht en de warmte van deze energiebronnen ioniseren het overgebleven gas.
- Het tijdperk van het licht (tot nu, ongeveer 13 miljard jaar, temperatuur 2,7 K).
- Het oorspronkelijke gas is gaandeweg verbruikt en steeds sterker vervuild geraakt met zware elementen die afkomstig zijn van de ::sterren.
- De laatste paar miljard jaar neemt de stervorming steeds verder af; bijna alle quasars zijn verdwenen en de vorming van nieuwe ::sterrenstelsels vindt nog maar zelden plaats.
- In dezelfde periode is er op aarde leven ontstaan, dat zeer kort geleden intelligentie heeft voortgebracht.
- De toekomst
- Het heelal koelt af, de sterren sterven en de kosmische activiteit zal afnemen.
- Maar de strutctuurvorming heeft een open einde en wordt steeds ingewikkelder aangezien grotere structuren mogelijk zullen worden en ::teglijkertijd steeds meer zwaartekrachtenergie beschikbaar komt.
Het uitdijen van het heelal[bewerken]
Op grote schaal gezien dijt het heelal uit en bestaat het uit groepen sterrenstelsel die allemaal van elkaar weg bewegen. Sterrenstelsels hebben een enorme omvang en bestaan doorgaans uit meer dan een miljard sterren, maar toch zijn ze veel kleiner dan de voor ons waarneembare ruimte (die ongeveer honderd miljard steerrenstelsel bevat). Het ligt dus voor de hand om het heelal te beschouwen als een uitdijende verzameling sterrenstelsel. de ze voorstelling vormt de kern van het oerknal model.
http://forum.fok.nl/templates/foksilver/i/p/5.gif Dijt alles uit?[bewerken]
De gedachte dat het heelal in zijn geheel uitdijt, lijkt vreemd omdat wij het heelal slechts op kleine schaal ervaren, waar het georganiseerd is in min of meer stabiele eenheden van materie zoals planeten, sterren en sterrenstelsels. Materie op kleine schaal dijt niet uit: jij en ik zijn stabiele structuren van atomen. Het zonnestelsel dijt niet uit, het is een (bijna) stabiel geheel van planeten die in hun baan worden gehouden door de zwaartekracht van de zon: de planeten bewegen, maar ze doen dat jaar in jaar uit op ongeveer dezelfde manier. En ook sterrenstelsels zijn stabiele verzamelingen sterren en andere materie die door de zwaartekracht bijeen worden gehouden. Tot op zekere hoogte draaien ook sterrenstelsel om elkaar heen in grote clusters. Maar op zeer grote schalen (stel je een zeer onduidelijke film voor waarbij je alleen de algemene beweging van grote groepen sterrenstelsels kunt onderscheiden) dijt die enorme wolk sterrenstelsels uit en beweegt elk onderdeel zich weg van het andere.
Deze beweging heeft te maken met de bijna-uniformiteit van materie op grote schaal en met het feit dat alle richtingen in de ruimte gelijkvormig zijn. De expansie ondergraaft de gelijkvormigheid niet: een uniform uitdijend systeem kan, hoewel het in beweging is, toch gelijkvormig blijven (al dunt het uit met de tijd) zonder een bepaalde richting te kiezen. Rotatie kiest bijvoorbeeld een richting in de ruimte, en ook niet-uniforme samendrukking en verdunning doen dat. De uitdijing is dus een weerspiegeling van de eenvoud van het heelaal op zeer grote schaal en in vroege tijden; het is het eenvoudigste gedrag dat een heelal kan vertonen. Lang geleden, kort na de oerknal, was het heelal gelijkvormig op een veel kleinere schaal, en zelfs zeer kleine delen ervan vlogen toen van elkaar weg; n�g eerder vlogen zelfs zaken die enkele centimeters van elkaar verwijderd waren uit elkaar. Nu is materie op kleine schaal gestold in stabiele systemen die niet meer uitdijen, want daar voltrok de expansie zich minder snel en hebben krachten haar tot staan gebracht. Op deze kleinere schalen zijn de dingen niet meer gelijkvormig: de materie heeft sterrenstelsels gevormd die zich van elkaar verwijderen maar zelf niet uitdijen.
http://forum.fok.nl/templates/foksilver/i/p/5.gif Bevinden wij ons in het centrum van het Heelal?[bewerken]
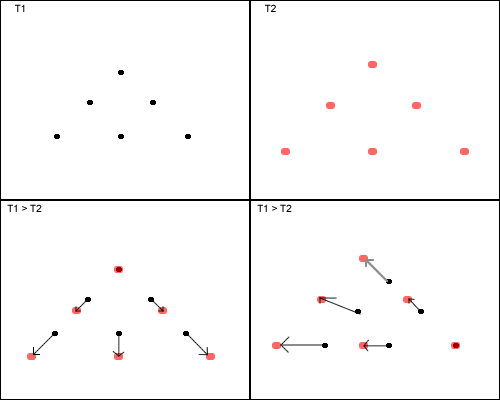
Ogenschijnlijk bevinden wij ons in het centrum van het heelal, maar dat lijkt zo te zijn vanuit elk sterrenstelsel, op elke plek en op elk moment. Vreemd genoeg bevindt het centrum zich zowel overal als nergens. ruimte is driedimensionaal, maar het is makklijker om je de uitdijing tweedimensionaal of zelfs eendimensionaal voor te stellen. Denk bijvoorbeeld aan een doorgeknipt elastiek dat wordt uitgerekt en waarop zich kralen bevinden die de sterrenstelsels voorstellen. Vanuit elke kraal gezien verwijderen allen andere kralen zich. Het elastiek kan eeuwig worden uitgerekt en elke kraal kan als het centrum worden beschouwd. Hoe verder twee punten van elkaar verwijderd zijn, hoe sneller ze zich van elkaar weg bewegen.
Dit figuur geeft een tweedimensionale voorstelling van de uitdijing. Een aantal punten wordt getoond op twee momenten; de patronen zijn gelijk, maar het tweede is iets groter. Wanneer je de twee patronen op elkaar legt, hebben ze een duidelijk centrum, maar wanneer je een punt in T2 op hetzelfde punt in T1 legt, lijkt dat punt het centrum. De patronen zijn niet veranderd, alleen onze interpretatie van wat zich verplaatst heeft is veranderd. Net als in het elastiekvoorbeeld hebben puntent die verder uit elkaar liggen, zich tussen T1 en T2 verder van elkaar verwijderd, wat betekent dat ze sneller van elkaar weg bewegen.
In het echte heelal is het net als in dit voorbeeld, met dit verschil dat er nog een dimensie bij komt. Een dunne plak uit het universum gesneden zou een situatie te zien geven zoals in het bovenstaande figuur, een dunne (eendimensionale) 'reep' zou lijken op het elastiek dat wordt uitgerekt. Dat alles zich van ons verwijdert, betekent nog niet dat we ons in het centrum van het heelal bevinden. Elk punt is het centrum, of geen enkel punt, want het heele lijk vanuit elk punt uit te dijen.
http://forum.fok.nl/templates/foksilver/i/p/5.gif Waartoe leidt de uitdijing?[bewerken]
Heeft het heelal een einde? Misschien, maar niet noodzakelijk. Het is mogelijk dat het heelal steeds groter wordt, dat er staat meer ruimte komt zonder dat deze is ingebed in een andere, grotere ruimte. Misschien breidt het heelal zich eindeloos naar alle kanten uit, misschien kromt het in zichzelf terug, zoals een rubberen band of het oppervlak van een ballon. Hoe het ook zij, de uitdijing heeft alleen van binnenuit gezien betekenis - er is geen plaats 'buiten' vanwaar zij bezien kan worden. Mogelijk is er w�l een einde, maar dat moet dan ver voorbij het voor ons zichtbare heelal liggen. We hebben niets waargenomen wat op een einde lijkt, en eigenlijk ook niets wat er werkelijk anders uitziet dan ons deel van het heelal. Als de oerknal een brok dynamiet is dat explodeert, dan bevindt alles wat wij zien zich binnen deze explosie.
Het waarneembare universum heeft echter wel een grens, want door de eindige leeftijd ervan wordt wat wij kunnen zien van de ruimte beperkt. Wanneer wij het heelal in kijken, kijken we terug in de tijd (namelijk de hoeveelheid tijd die het licht nodig had om ons te bereiken): een paar seconden naar de maan, acht minuten naar de zon, jaren of duizenden jaren naar sterren in ons sterrenstelsel en ongeveer twee miljoen jaar naar de verst van ons verwijderde nevel die nog met het blote oog waarneembaar is, namelijk de Andromedanevel (M31). Het verste wat we kunnen zien - per definitie - heeft het licht wat we nu zien kort na de oerknal uitgezonden. Dat licht is dus bijna de gehele geschiedenis van het heelal naar ons onderweg geweest. We kunnen nooit verder kijken dan dat, of beter: we zullen moeten wachten om verder te kunnen kijken, een jaar voor elk lichtjaar extra. Omdat het heelal slechts 12 tot 15 miljard jaar oud is, kunnen de verste objecten (ervan uitgaande dat het heelal al die tijd aan het uitdijen is geweest) inmiddels niet verder van ons verwijderd zijn dan 20 tot 30 miljard lichtjaar. In die zin heeft het heelal wel een grens, maar het is eerder een grens in de tijd dan in de ruimte. Om een voorbeeld te geven: een van de 'diepste' beelden die we nu zien is de vorming van enkele van de eerste sterrenstelsels. Het is opmerkelijk dat alle plekken in deze enorme ruimte zeer sterk op elkaar lijken: overal zijn sterrenstelsels en het heelal lijkt nergens te eindigen.
http://forum.fok.nl/templates/foksilver/i/p/5.gif Wat gebeurde er voor de oerknal?[bewerken]
De vraag naar wat er gebeurde voor de oerknal heeft twee componenten: een mechanistische over het uitdijinde heelal en een andere over de tijd zelf. Wij weten niet genoeg over de vroegste momenten van de oerknal, mede doordat we niet alle natuurkundige processen kennen (waaronder die met de betrekking tot de tijd) die zich hebben afgespeeld.
Waarom w�s er een oerknal? Volgens een van de hypothesen (de inflatiehypothese) ontwikkelde zich uit het fysische vacu�m van de lege ruimte een zeer sterk afstotende zwaartekracht (heeft te maken met kwantumfluctuaties wat nogal ingewikkeld is). Deze dreef de energie van het heelal uiteen in een explosie die de oerknal in gang zette. Alles wat nodig was om een enorm, uitdijend heelal te doen ontstaan was een microscopisch stukje aangeslagen vacu�m. Daarna moest de oerknal plaatsvinden, want dat schrijven de natuurkundige wetten voor.
Veel idee�n over de inflatie zijn inmiddels gemeengoed geworden. De gedachte van een afstotende vacu�mzwaartekracht gaat terug op Einsteins vroege publicaties over de kosmologie; het verband met de kosmische uitdijing werd gelegd in de jaren 30 (niet veel later dan de ontdekking van de uitdijing) door Arthur Eddington, een vroege voorvechter van Einsteins gravitatietheorie. En het concept van een aangeslagen vacu�m past goed in de moderne deeltjesfysica. Maar hoewel er veel gedetailleerde theori�n zijn over hoe de inflatie in zijn werk is gegaan, is er geen standaardmodel dat verklaart waar de eerste kwantumfluctuatie vandaan kwam. Dit is niet zo verbazingwekkend en vanuit een natuurkundig oogpunt doet het er niet erg toe want bijna alle informatie uit die tijd is verloren gegaan. Het was niet meer dan een fluctuatie, van weinig belang behalve dan dat zij het begin was van het universum. Met andere woorden, het universum schiep zijn eigen informatie, het maakte zichzelf interessant, dus het is onverstandig al te lang te blijven stilstaan bij die aanvankelijke fluctuatie, alsof die de eer zou moeten krijgen voor alles wat erna gebeurd is. En als die aanvangsfluctuatie min of meer irrelevant is en we er tich niet over te weten kunnen komen, moeten we ons het hoofd er niet over breken en gewoon verdergaan.
http://forum.fok.nl/templates/foksilver/i/p/5.gif Heeft de tijd zelf een begin gehad?[bewerken]
In tegenstelling tot wat onze intu�tie ons influistert (die waarschijnlijk is gebaseerd op onze ervaring dat het ene tijdsinterval veel op het andere lijkt) is de tijd zoals wij die kennen naar het verleden toe mogelijk niet oneindig. Net als bij de ruimte hoeft dit niet per se te betekenen dat er een uiterste grens is (een vroegste moment waaraan geen enkel moment voorafging). Het is zeer goed vol te houden dat de begrippen 'voor' en 'na' niet meer van elkaar te onderscheiden zijn als je maar ver genoeg teruggaat. Tijd heeft dan niet meer dezelfde betekenis als in de gewone natuurkunde. We hebben reeds vastgesteld dat het conventionele begrip 'tijd' niet van toepassing is op zeer kleine intervallen, dus als het begin te dicht wordt benaderd, kunnen we dit begrip niet meer gebruiken. 'Tijd' en 'ruimte' zijn concepten die alleen zinvol zijn met betrekking tot bepaalde minimale afmetingen en intervallen. Er zijn wel ontwerpen voor beschrijvingen van kleinere ruimten en tijdsintervallen (wat dat ook moge betekenen ), maar geen enkel is getoetst aan de werkelijkheid. Je kunt dit vergelijken met de middeleeuwse speculaties over het einde van de wereld. Iemand die denkt dat de aarde plat is, verwacht ofwel een oneindige ofwel een begrensde wereld te vinden, maar bij een ronde aarde wordt de vraag naar het einde ervan zinloos. Zich afvragen wat er was voor de oerknal is misschien hetzelfde als vragen wat er ten noorden van de noordpool ligt (waar het begrip 'ten noorden van' geen betekenis heeft). Het is aanmatigend om te veronderstellen dat onze idee�n over de tijd, die gebaseerd zijn op de huidige situatie van het heelal, ook zouden moeten gelden voor de uiterste grenzen van de ruimtetijd.
Het is ook mogelijk de de aanvangsfluctuatie deel was van een ander, groter heelal. In dat geval gaat de tijd misschien eindeloos terug en is hij misschien zelf ingebed in andere universa. Maar het is niet waarschijnlijk dat we ooit informatie zullen vergaren over wat zich 'hiervoor' afspeelde - dus het getuigt eigenlijk van een middeleeuwse inborst om te blijven stilstaan bij deze mogelijkheid. Maar deze kwesties doen niet zo ter zake wanneer we het oerknalmodel en de daaruit voortkomende voorspellingen bespreken. Alle inflatiemodellen gaan ervan uit dat �ls er iets geweest is 'voor' de oerknal, het bewijs hiervan lang geleden is vernietigd of vervaagd. De structuur van het hedendaagse heelal op de grootste schaal weerspiegelt waarschijnlijk de inflatieperiode en gebeurtenissen in het wat oudere heelal; de samenstelling van het heelal weerspiegelt de thermische heksenketel van de oerknal na de inflatie; en de complexiteit van de structuren op grote schalen (van moleculen tot sterrenstelsels) weerspiegelt miljarden jaren kosmische evolutie. Dat zijn zaken die we, met behulp van waarnemingen en de modellen. kunnen bestuderen.
De structuur van een vierdimensionale ruimtetijd kan gevisualiseerd worden als we bereid zijn enkele dimensies te laten vallen. In deze visualisatie is het begin weergegeven als een punt, aangezien alles toen zeer dicht opeengepakt zat. De horizontale doorsneden worden steeds groter en geven de totale ruimte op een bepaald moment weer (in een bepaald model), waarbij twee van de drie ruimtedimensies zijn weggelaten. De schaal is natuurlijk enorm: de 'doorsnede' heeft momenteel bijvoorbeeld een omtrek van ten minste tientallen miljarden lichtjaren.
In een andere visualisatie is de uitdijing weggelaten en worden de huidige posities getoond van zaken die in het verleden hebben plaatsgevonden en nu worden waargenomen. Het is een weergave van de 'verleden lichtkegel': de gebeurtenissen die we zien door in de ruimte en terug in de tijd te kijken. Elke horizontale doorsnede stelt een verzameling gebeurtenissen voor in een wijde cirkel om ons heen. Dit model laat beter de begrenzing zien van het terugkijken naar het begin van de tijd. De afstand naar deze kosmische horizon is weer tientallen miljarden lichtjaren. Hoewel deze slechts modellen zijn van mogelijk ruimtetijden, kunnen we de globale structuur van het huidige heelal in kaart brengen door het licht te observeren dat afkomstig is van ver verwijderde objecten.
http://forum.fok.nl/templates/foksilver/i/p/4.gif Effecten van de uitdijing op licht.[bewerken]
Licht dat door het uitdijend heelal reist, ondergaat veranderingen ten gevolge van die uitdijing. De golflengten van het licht dat afkomstig is van verre sterrenstelsels zijn tegelijk met het heelal uitgerekt. Blauw licht wordt geel na ongeveer 20 procent uitdijing, en rood na nog eens 20 procent. Na zeer lange tijd, dat wil zeggen na nog eens duizend keer zoveel uitdijing, is het zichtbare licht veranderd in microgolven, en na honderd keer meer uidijing in radiogolven. De uitdijing heeft een 'afkoelend' effect op het oorspronkelijke licht. Het heelal begon zeer heet en gevuld met hoogenergetische straling met een een korte golflengte, die nu grotendeels is afgekoeld tot laagenergetische microgolven. Licht dat afkomstig is van verder weg gelegen sterrenstelsels is langer geleden uitgezonden en vertoont meer 'roodverschuiving' (uitrekking), wat erop duidt dat het heelal in het verleden kleiner was; de sterrenstelsels bevonden zich dichter bij elkaar.
De golflengte van het licht dat zich voortplant in een uitdijend heelal worden, gelijk opgaand met de afmeting van het heelal, langer. De afmeting van het heelal op het moment dat het licht door een object werd uitgezonden, kan worden vastgesteld door de mate van roodverschuiving te meten van bepaalde aanvankelijk 'zuivere' kleuren van de 'favoriete' golflengten van atomen in sterrenstelsels die het licht hebben uitgezonden. Zo'n zuivere kleur is het intense rood van de laserstraal in een cd-speler of de codescanner in een supermarkt. De golflengte hiervan is altijd exact dezelfde, want de lasers zijn van hetzelfde materiaal gemaakt. wanneer je er een zou zien die roder was, zou er sprake zijn van roodverschuiving. Door de mate van roodverschuiving van een zuivere kleur te meten, kan dus worden bepaald hoeveel het heelal is uitgedijd in de tijd dat het licht naar ons onderweg was. De meest verafgelegen objecten vertonen de grootste roodverschuiving: het licht dat ze hebben uitgezonden is maximaal uitgerekt.
De helderste dingen in het heelal, en dus de gemakkelijkst bestudeerbare op grote roodverschuiving, zijn quasars: extreem sterke energiebronnen in de centra van sterrenstelsels. De golflengte van het licht van de verst verwijderde quasar die wij nu waarnemen is zes keer zo groot als toen het de quasar verliet. Het heelal had toen ongeveer een zesde van zijn huidige afmeting. Licht dat afkomstig is van vroegere tijden is nog veel meer uitgerekt. Het licht van de oerknal is nog afkomstig van voor de ontkoppeling van de zwakke wisselwerking, toen het heelal minder dan een miljardste van zijn huidige omvang had en meer dan tien miljard keer zo heet was.
http://forum.fok.nl/templates/foksilver/i/p/4.gif De wet van Hubble en de mate van uitdijing[bewerken]
De golflengteverandering van het licht kan worden vergeleken met de veranderingen van het geluid van bewegende objecten: wanneer een ambulance met loeiende sirene op ons af rijdt, is het geluid hoger dan wanneer de ambulance zich van ons verwijdert. De roodverschuiving van het licht is gelijk aan de verwijderingssnelheid gedeeld door de snelheid van het licht. Als de verwijderingssnelheid niet te groot is, kan de kosmische roodverschuiving worden voorgesteld door de wet van Hubble, die de relatieve verwijderingssnelheid en de onderlinge afstand van twee sterrenstelsels met elkaar in verband brengt:
Snelheid = H0 x afstand
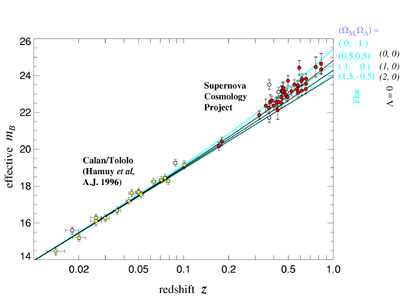
Zoals ook in het elastiekmodel werd ge�llustreerd, bewegen stelsels zich sneller van elkaar weg wanneer ze verder van elkaar verwijderd zijn. De wet van Hubble geeft de werkelijkheid goed weer, zoals uit het Hubble-diagram blijkt.
In dit diagram worden afstand en snelheid of roodverschuiving tegen elkaar uitgezet. Het getal H0 in deze formule is de Hubble-constante, die gevonden kan worden door niet relatieve afstanden maar absolute afstanden te bepalen. Als de wet van Hubble klopt, kunnen we de Hubble-constante bepalen door de verwijderingssnelheid (of roodverschuiving) en de afstand van het sterrenstelsel tot ons te meten. Snelheden kunnen zeer precies bepaald worden aan de hand van de roodverschuiving van het licht. Afstanden kunnen ook nauwkeurig bepaald worden, als ze niet te groot zijn, en wel met behulp van driehoeksmeting, een techniek die ook door landmeters wordt gebruikt.
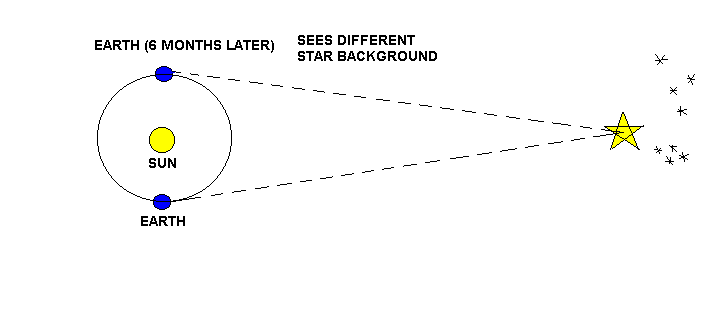
De afstand tot nabije sterren kan berekend worden door de omloopbaan van de aarde als basislijn te nemen; de gezochte afstand vind je door de kleine verschillen in positie door het jaar heen te meten ten opzichte van zeer ver weg gelegen sterren. Hiermee kunnen kleine kosmische afstanden worden berekend, maar voor grote afstanden is deze methode niet bruikbaar (de hoeken zijn daarvoor te klein). En aangezien de wet van Hubble geldt voor globale bewegingen op grote schaal, is het om de Hubble-constante te kunnen bepalen noodzakelijk om de grote afstanden nauwkeurig te meten, wat technisch een zeer moeilijke opgave is. Dat is de reden dat de waarde van de Hubble-constante nog altijd een onzekerheidsmarge van ongeveer 20 procent heeft, hoewel het lieaire karakter van de wet van Hubble al wel tamelijk nauwkeurig is aangetoond. De waarde van de Hubble-constante is belangwekkend omdat hij ons vertelt hoe snel objecten zich van elkaar verwijderen. Omdat de verwijderingssnelheid recht evenredig is met de afstand, zou elk sterrenstelsel er, in omgekeerde richting, even lang over doen om de afstand naar willekeurig welk ander sterrenstelsel te overbruggen. Met ��n enkel getal, het omgekeerde van de Hubble-constante, 1/H[sub]0[/sub], kan dus uitgedrukt worden hoe lang geleden alle sterrenstelsels 'op dezelfde plaats' waren, aangenomen dat de uitdijingssnelheid altijd gelijk is geweest (discutabel). Volgens de huidige berekeningen ligt 1/H[sub]0[/sub] tussen de 14 en 17 miljard jaar. Als de sterrenstelsels nooit van snelheid zijn veranderd, moeten ze zich zo lang geleden op punt 0 hebben bevonden en is dit de hoeveelheid tijd die is verstreken sinds de oerknal.
http://forum.fok.nl/templates/foksilver/i/p/4.gif Veranderingen in de uitdijingssnelheid[bewerken]
Maar sterrenstelsels, en de pregalactische materie daarvoor, hebben niet altijd dezelfde uitdijingssnelheid gehad. De snelheid is be�nvloed door de zwaartekracht. Wanneer je een voetbal de lucht in schiet, zal hij terugvallen naar de aarde, behalve wanneer hij zeer hard wordt geschoten: dan zal hij worden afgeremd maar nooit terugvallen en zich eeuwig verwijderen van de aarde. Dezelfde opties gelden voor het heelal; het zijn ook dezelfde wiskundige vergelijkingen die de beweging van de voetbal en de verwijdering van twee sterrenstelsels beschrijven. Het natuurkundige principe is hetzelfde: in beide gevallen wordt de beweging bepaald door de zwaartekracht. Het enige verschil is dat de beweging van de bal wordt bepaald door de zwaartekracht van de aarde en de beweging van de sterrenstelsels door de zwaartekracht van hun eigen massa en die van ander materiaal in het heelal. Vergelijkbaar met de zacht geschoten bal is een langzaam uitdijend heelal met een grote dichtheid. De uitdijingssnelheid van zo'n heelal neemt af tot de uitdijing uiteindelijk stopt; daarna krimpt het weer in en beginnen alle sterrenstelsels naar elkaar toe te bewegen om te eindigen in een 'eind-krak'. De hard geschoten bal is vergelijkbaar met een snel uitdijend heelal met een lagere dichtheid dat eeuwig blijft uitdijen. De sterrenstelsels dunnen dusdanig uit dat de zwaartekracht niet veel effect meer heeft. Wanneer zo'n heelal zeer oud wordt, neemt de uitdijingssnelheid nauwelijks nog af en blijft het heelal met een bepaald kruissnelheid uitdunnen. Tussen deze twee scenario's ligt het delicate evenwicht van een heelal dat te vergelijken is met de voetbal die precies de ontsnappingssnelheid heeft meegekregen: het juiste evenwicht tussen snelheid en dichtheid zorgt ervoor dat het heelal eeuwig snelheid 0 nadert maar nooit bereikt.
Net als met de bal is het moeilijk te bepalen welk scenario voor het heelal geldt alleen door naar de situatie op een bepaald moment te kijken. Als de bal maar een klein stuk omhoog wordt geschoten, zal hij direct weer terugvallen, maar als hij hard wordt geschoten, zal hij zeer ver komen voordat hij terugkeert - en het is moeilijk te zeggen �f hij zal terugkeren. Ook een heelal kan zeer lang uitdijen voordat het, als dat al gebeurt, weer gaat inkrimpen. Als dat het lot van ons heelal is, zal het eerst tientallen miljarden jaren hebben bestaan. De ontsnappingssnelheid van de bal is afhankelijk van de massa van de aarde en van de hoogte waarvandaan hij geschoten is. Zo is ook het lot van het heelal afhankelijk van de snelheid waarmee het uitdijt en de hoeveelheid massa die de uitdijing vertraagt. Deze waarden zijn nog niet exact genoeg bepaald om te kunnen weten wat er gebeuren zal. De beste methode om ze te bepalen is door de expansiesnelheid in het verleden vast te stellen (door zeer ver weg te kijken) en deze te vergelijken met de huidige snelheid. De gegevens zijn nog niet betrouwbaar genoeg om te kunnen zeggen dat de uitdijingssnelheid afneemt, maar er zijn veelbelovende technieken.
Het heelal heeft echter nog een optie die de bal niet heeft, namelijk om steeds sneller te gaan uitdijen, zoals een bal in een slingerworp of een raket. Dit is in principe mogelijk doordat de zwaartekracht als een afstotende kracht kan inwerken op lege ruimte. Einstein introduceerde deze mogelijkheid van een 'kosmologische constante' kort na zijn gravitietheorie. Deze treedt op als lege ruimte zonder materie of straling toch energie bevat, waarop de zwaartekracht aangrijpt. Als het vacu�m genoeg energie heeft, zal de kracht die het heelal uiteendrijft de zwaartekracht overvleugelen en zal de uitdijingssnelheid met de tijd toenemen. Deze optie is al sinds de ontdekking van de uitdijing bekend, maar we weten nog altijd niet zeker of de uitdijingssnelheid toeneemt of afneemt (hoewel de laatste onderzoeken het eerste aantonen). Alleen door de dynamica op zeer grote schalen te onderzoeken lijkt het mogelijk om de energie van het vacu�m te bepalen.
http://forum.fok.nl/templates/foksilver/i/p/4.gif De leeftijd van het heelal[bewerken]
Zelfs als we de Hubble-constante en de Hubble-tijd (de tijd die alle sterrenstelsels nodig hadden om te komen waar ze nu zijn met hun huidige snelheid) kennen, weten niet precies hoe oud het heelal is. De leeftijd is afhankelijk van de veranderingen in de uitdijingssnelheid door de tijd heen, en die zijn weer afhankelijk van de soorten en de hoeveelheid materie die het heelal bevat. Maar we kunnen het omdraaien: als we de leeftijd met de Hubble-tijd ons iets vertellen over de aard van het universum en de toekomst ervan. We weten vrij nauwkeurig hoe oud ons zonnestelsel is: de zon, de aarde en andere planeten zijn ongeveer 4,55 miljard jaar geleden uit interstallair gas gevormd. Deze schatting is gebaseerd op metingen van radioactief verval. De atoomkernen van sommige elementen, zoals uranium-238, zijn instabiel en verallen tot atoomkernen van andere elementen. Dat doen ze met een bepaalde snelheid die heel precies te bepalen is. Na 4,6 miljard jaar bijvoorbeeld heeft een atoom uranium-238 50 procent kans om te zijn vervallen tot lood-206 en bestaat een oorspronkelijk pure klomp uranium-238 voor de helft uit lood-206. Als we dus vrij voorkomende stukken steen en meteorieten die uranium bevatten maar zonder lood-206 zijn begonnen (of met een hoeveelheid andere isotopen van lood), dan is uit het percentage lood-206 af te leiden hoe lang geleden het uranium werd gevormd. Zeer veel objecten uit ons zonnestelsel, vooral meteorieten, zijn onderzocht op verschillende soorten radioactief verval (bijvoorbeeld van kalium-40 naar argon-40; halveringstijd 1,3 miljard jaar). Alle berekeningen komen uit op dezelfde leeftijd van 4,55 miljard, dus het zonnestelsel is minstens zo oud.
Hoewel er nog steeds sterren worden gevormd, zijn er vele die ouder zijn dan ons zonnestelsel. Sommige zijn twee tot drie keer zo oud en het is waarschijnlijk dat een aantal van de eerste sterren die ontstaan zijn na deoerknal nu nog brandt. We kunnen deze sterren gebruiken om te schatten hoe oud het heelal is.
Het zou prettig zijn geweest als iemand een stopwatch had aangezet bij de oerknal en hem voor ons had achtergelaten zodat wij gewoon de hoeveelheid tijd die is verstreken konden aflezen. In feite hebben we iets wat hierop lijkt: oude groepen sterren met een grote verscheidenheid aan massa's die als een soort zandlopers met verschillende snelheden lopen. Als we dus in staat zijn sterren als zandlopers te lezen, dat wil zeggen: te bepalen hoe oud ze zijn aan de hand van onze kennis van hun levensloop, dan kunnen we ook de leeftijd van de clusters waartoe ze behoren bepalen door naar de zandlopers te kijken die bijna leeggelopen zijn. Om dat te kunnen doen hebben we een model van de werking van sterren nodig.
Sterren als onze zon, die genoeg brandstof hebben. blijven miljarden jaren stabiel. Het zijn gasbollen die grotendeels bestaan uit waterstofatomen en vrije elektronen en die bijeen worden gehouden door de zwaartekracht en voor instorten behoed door de hitte van de nucleaire reacties in hun kern. De meeste sterren brengen het grootste deel van hun leven door in deze fase en de meeste sterren die wij aan de hemel zien bevinden zich in deze fase.
Maar deze stabiele toestand eindigt uiteindelijk. Het evenwicht dat de ster in stand houdt, begint te wankelen wanneer de waterstof in de kern, die als brandstof dient, begint op te raken. Door dit tekort stort de kern in. Hierbij komt meer hitte vrij dan nodig is om de buitenste lagen in stand te houden zodat deze naar buiten worden gedreven. De structuur van de ster verandert dus als de waterstof opraakt: de kern wordt kleiner, de buitenste lagen groter. De effecten hiervan zijn zichtbaar in het licht dat de ster uitzendt. Omdat het licht afkomstig is van een groter gebied, is het meer verspreid, waardoor ook de temperatuur anders is. De ster wordt koeler en zijn licht wordt roder.
Sterren lijken op zandlopers omdat ze vanaf het moment dat ze zijn gevormd hun brandstof beginnen te verbruiken. Wanneer die begint op te raken veranderen ze van kleur. Zware sterren schijnen helderder dan lichte en verbruiken hun brandstof sneller (ze werken als snellere zandlopers). Van een groep sterren zullen de zwaarste dus het eerste uitdoven. Door de massa te meten van de sterren die net door hun brandstof heen zijn, kunnen we de leeftijd van de cluster vaststellen.
We kunnen sterren aflezen als klokken omdat we weten hoe ze zich ontwikkelen. Er zijn modellen ontwikkeld die voor elke massa en samenstelling van een ster bepaalde waarneembare eigenschappen (helderheid en kleur) voorspellen bij een bepaalde leeftijd. Uit de helderheid en kleur van een ster kunnen we dus afleiden hoe lang geleden hij is gevormd. De nauwkeurigheid van deze modellen is bevestigd door andere tests. De voorspelde leeftijd van de zon komt bijvoorbeeld overeen met de resultaten van datering met behulp van radioactief verval. En als de massa van een ster bekend is, kunnen de helderheid en kleur ervan voorspeld worden. Er is zelfs een geval bekend waarbij twee om elkaar draaiende sterren met een verschillende massa volgens de berekeningen even oud zijn.
Momenteel wordt de leeftijd van de oudste sterrenhopen geschat op 12 tot 15 miljard jaar. De oudste sterrenhopen lijken maar een paar miljard jaar van elkaar te verschillen in leeftijd en er is niet veel gevonden wat ouder is dan dit - een opmerkelijk feit, wat waarschijnlijk betekent dat het heelal ongeveer zo oud is. Nog opmerkelijker is dat deze leeftijd overeenkomt met de expansietijd van 14 tot 17 miljard jaar die is afgeleid van de Hubble-constante. We hebben nu dus een behoorlijk betrouwbaar beeld van de kosmische chronologie, al zijn de marges nog vrij ruim.
Als we goed naar de getallen kijken, lijken de sterren in sommige modellen van de uitdijing (bijvoorbeeld de modellen waarbij het heelal weer gaat inkrimpen omdat de zwaartekracht de uitdijingssnelheid continu vertraagt) ouder te zijn dan het heelal. De voorspelde leeftijd van het heelal in alle 'eindkrakmodellen' is maximaal (2/3)/H[sub]0[/sub], ongeveer 10 miljard jaar. De leeftijd in deze modellen is betrekklijk jong omdat er wordt aangenomen dat de sterrenstelsels vroeger sneller uiteenvlogen dan nu. Ze hebben er dus minder lang over gedaan om te komen waar ze nu zijn en voorspellen dus een te jong heelal.
Het heelal kan oud zijn als de dichtheid van de materie laag is, zodat de uitdijing de laatste 10 miljard jaar nauwelijks door de zwaartekracht is vertraagd. En als de uitdijing zich heeft versneld ten opzichte van de kosmologische constante, dan voltrok zij zich daarvoor langzamer en kan het heelal nog ouder zijn. Hoe het ook zij, volgens de huidige opvattingen is er niet genoeg zwaartekracht om de uitdijing te stoppen en om te keren. Het heelal zal waarschijnlijk nog zeer lange tijd uitdijen, en mogelijk zelfs voor eeuwig.
Het naakte feit van de uitdijing impliceert dat de materie ooit een veel grotere dichtheid had dan nu. Het huidige verloop van de uitdijing vertelt ons echter niet veel over het gebeuren tijdens de eerste miljard jaar, de eerste miljoen jaar, de eerste minuten, de eerste seconden. De twee belangrijkste bronnen van informatie over deze perioden van de kosmische geschiedenis zijn de kosmische achtergrondstraling en de samenstelling van de oermaterie.